3.3 Interne Funktionsweise
Dieses Kapitel befasst sich ein wenig mit der internen Struktur des CNF-DNF-Konverters und damit, wie dieser mit aussagenlogischen Formeln arbeitet.
Abbildung:
Klassendiagramm der Datenstruktur für aussagenlogische Formeln
|
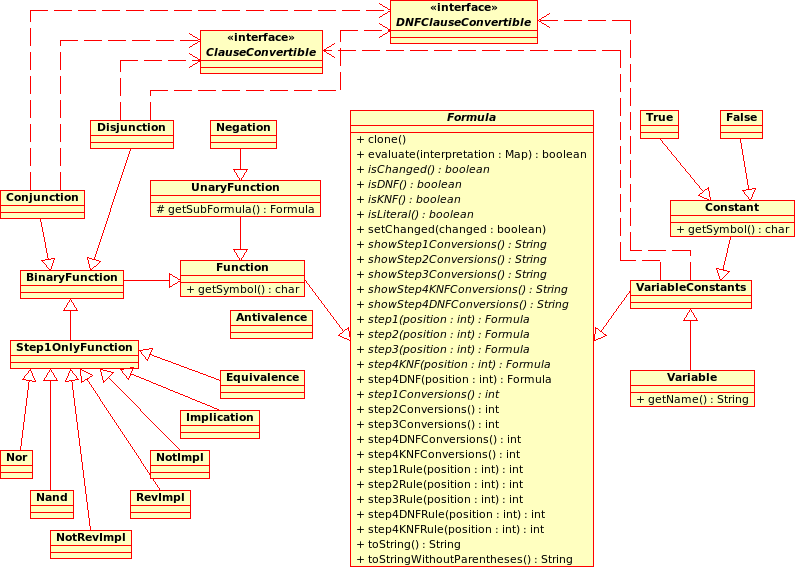 |
Abbildung 10 zeigt die Klassenstruktur, die zur Speicherung aussagenlogischer Formeln in einer leicht verarbeitbaren Form verwendet wird. Jede aussagenlogische Formel wird als Instanz der Klasse Formula gespeichert. Formula bietet unter anderem Funktionen, um
- eine Formel schrittweise in ihre äquivalente KNF und DNF umzuformen,
- zu prüfen, ob noch ein bestimmter Umformungsschritt möglich ist oder
- aussagenlogische Formeln unter einer gegebenen Interpretation auszuwerten.
Um aus einer Texteingabe eine Instanz von Formula zu erhalten, verwendet der KNF-DNF-Konverter eine Kombination von Scanner (JFlex
(JFlex
sowie Parser
(CUP
Die Grammatik, auf welche bereits in den vorhergehenden Kapiteln Bezug genommen wurde, ist die Grammatik 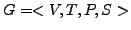 , die in Abbildung 11 beschrieben wird.
, die in Abbildung 11 beschrieben wird.
Neben der Datenstruktur, die auf Formula aufbaut, gibt es weiters Datenstrukturen, die eine Formel in KNF beziehungsweise DNF in Mengennotation repräsentieren. Instanzen von Subklassen von Formula, die das Interface ClauseConvertible oder DNFClauseConvertible implementieren, können, sofern es sich bei dieser Instanz um die Repräsentation einer Formel in KNF oder DNF handelt, in Mengennotation übertragen werden. Eine Formel in Mengennotation kann auch wieder in eine aussagenlogische Formel in ,,herkömmlicher Darstellung” konvertiert werden.
Das Besondere an dieser Mengennotation im CNF-DNF-Konverter ist einerseits, dass sie nicht nur, wie im Skriptum zur Lehrveranstaltung Theoretische Informatik und Logik, für Formeln in KNF, sondern auch für Formeln in DNF Verwendung findet. Der Sinn dahinter ist jener, dass in Mengennotation Vereinfachungen der Formel leichter möglich sind. Dazu wird die Formel zunächst in Mengennotation übertragen, dann werden die unten beschriebenen Vereinfachungen durchgeführt und die Formel wird wieder in ,,normale Darstellung,, übertragen.
Die unten beschrieben Vereinfachungsschritte werden dabei vom Programm durchgeführt. Die Erlärungne, die als Begründungen für die Korrektheit der einzelnen Umformungsschritte gegeben werden, sind rein informativer Natur und nicht als formale Beweise anzusehen.
- Eliminieren von Duplikaten (aus Multimengen werden ,,echte” Mengen): Aus
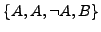 wird
wird
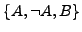 , aus
, aus
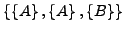 wird
wird
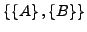 .
.
- Eliminieren von Tautologien (KNF): Unter der Annahme, dass es sich bei der Klauselmenge
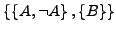 um die Repräsentation einer Formel in KNF handelt, entspricht diese Menge der aussagenlogischen Formel
um die Repräsentation einer Formel in KNF handelt, entspricht diese Menge der aussagenlogischen Formel
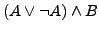 . Die Teilformel
. Die Teilformel 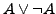 wertet unter jeder Interpretation zum Wahrheitswert
wertet unter jeder Interpretation zum Wahrheitswert
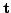 aus; eine solche Formel nennt man Tautologie. Da weiters
aus; eine solche Formel nennt man Tautologie. Da weiters
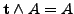 gilt für jede aussagenlogische Formel
gilt für jede aussagenlogische Formel 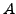 , ist
, ist
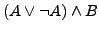 äquivalent zu
äquivalent zu 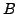 . Jede Klausel, die sowohl eine Variable als auch eine Negation enthält, repräsentiert eine Tautologie und kann daher weggestrichen werden.
. Jede Klausel, die sowohl eine Variable als auch eine Negation enthält, repräsentiert eine Tautologie und kann daher weggestrichen werden.
- Eliminieren von Kontradiktionen (DNF): Repräsentiert eine Menge von Literalmengen eine aussagenlogische Formel in DNF, so kann man die Menge
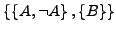 als
als
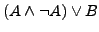 anschreiben. Hier wertet
anschreiben. Hier wertet 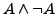 immer zum Wahrheitswert
immer zum Wahrheitswert
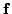 aus; eine solche Formel wird als Kontradiktion bezeichnet. Außerdem gilt
aus; eine solche Formel wird als Kontradiktion bezeichnet. Außerdem gilt
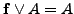 für jede aussagenlogische Formel
für jede aussagenlogische Formel 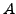 , daher ist
, daher ist
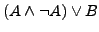 äquivalent zur Formel
äquivalent zur Formel 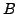 . Wie bei der KNF kann daher jede Literalmenge, die sowohl ein Literal sowie dessen Negation enthält, weggestrichen werden, da diese Menge eine Kontradiktion darstellt.
. Wie bei der KNF kann daher jede Literalmenge, die sowohl ein Literal sowie dessen Negation enthält, weggestrichen werden, da diese Menge eine Kontradiktion darstellt.
- Subsumtion: Seien
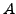 ,
, 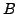 und
und 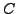 beliebige aussagenlogische Formeln. Wertet unter einer beliebigen Interpretation
beliebige aussagenlogische Formeln. Wertet unter einer beliebigen Interpretation 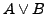 zu
zu
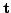 aus, so ist auch
aus, so ist auch
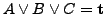 (wegen
(wegen
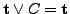 ). Das bedeutet, dass
). Das bedeutet, dass
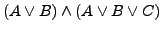 zu
zu
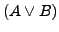 vereinfacht werden kann. Selbiges gilt für die Konjunktion: Wertet
vereinfacht werden kann. Selbiges gilt für die Konjunktion: Wertet 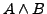 zu
zu
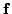 aus, so auch
aus, so auch
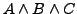 (wegen
(wegen
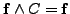 ). Daher kann
). Daher kann
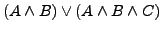 zu
zu
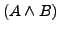 vereinfacht werden.
vereinfacht werden.
In Mengenschreibweise bedeutet das (unabhängig davon, ob diese Menge von Literalmengen eine Formel in KNF oder eine Formel in DNF repräsentiert), dass
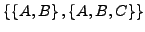 zu
zu
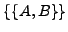 vereinfacht werden kann. Allgemeiner ausgedrückt: Eine Literalmenge
vereinfacht werden kann. Allgemeiner ausgedrückt: Eine Literalmenge 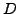 subsumiert eine andere Literalmenge
subsumiert eine andere Literalmenge 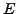 , falls
, falls 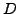 eine Teilmenge von
eine Teilmenge von 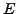 ist. Die Menge
ist. Die Menge 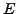 kann aus dem Ausdruck gestrichen werden, ohne den Wert des Ausdrucks unter irgendeiner Interpretation zu verändern.
kann aus dem Ausdruck gestrichen werden, ohne den Wert des Ausdrucks unter irgendeiner Interpretation zu verändern.
- Sortieren: Dieser Schritt vereinfacht die Mengen nicht, sondern sorgt lediglich für eine einheitliche Darstellung. Sortiert werden zunächst die einzelnen Literale innerhalb der Literalmengen und anschließend die Literalmengen selbst. Die Literale werden aufsteigend nach dem vorkommenden Variablennamen sortiert; kommen sowohl eine Variable als auch deren Negation in dem Ausdruck vor (was nach Entfernung von Tautologien beziehungsweise Kontradiktionen ohnehin nicht der Fall ist), so kommt das Literal, das keine Negation enthält, vor dem Literal, welches die Negation enthält.
Die Literalmengen werden aufsteigend nach dem Namen der im ersten Literal vorkommenden Variable sortiert. Ist dieser Name gleich, so kommt die Menge, in welcher das erste Literal eine nicht-negierte Variable ist, vor der Menge, in welcher das erste Literal eine negierte Variable ist. Ist dadurch keine eindeutige Sortierreihenfolge gegeben, werden die zweiten Literale der beiden Mengen verglichen. Ist eine Menge Untermenge einer anderen Menge (sollte nach Entfernung subsumierter Formeln im vorhergehenden Schritt ohnehin nicht mehr vorkommen), so kommt zuerst die Untermenge und dann die Obermenge.
Im Programm werden die Ergebnisse dieser Umformungsschritte nur für Formeln in KNF im Detail beschrieben, für Formeln in DNF bekommt der Benutzer lediglich die vereinfachte Form in ,,herkömmlicher Darstellung” zu sehen. Der Grund dafür ist jener, dass die Mengennotation in der Lehrveranstaltung Theoretische Informatik und Logik nur für aussagenlogische Formeln in KNF verwendet wird und daher die Teilnehmer dieser Lehrveranstaltung nicht durch die Verwendung der Mengennotation für Formeln in DNF im Programm verwirrt werden sollen.
Paul Staroch
2007-04-12

![]() , die in Abbildung 11 beschrieben wird.
, die in Abbildung 11 beschrieben wird.